1枚のA4サイズ紙を25回折ったら厚さ何センチ？

質問です。

『1枚のA4サイズの紙を半分ずつ25回折ったら、その厚さは何センチになるでしょうか？』

1枚のA4サイズの紙を半分ずつ25回折ったら、その厚さは何センチになるのか？

当てずっぽうでもいいので、ちょっと考えてみてください。

どのくらいになると思いますか？

ヒントは、A4コピー用紙1枚の厚さは、0.1mm です。

実際に計算してみよう。

「大体、このくらいかなあ？」と、あなたなりの答えはイメージできましたか？

それでは、実際に計算してみましょう。
A4コピー用紙1枚の厚さは0.1mmで半分ずつ折っていくわけですから、1回折ると0.2mmになり、2回折ると0.4mm、3回折ると0.8mmになります。

これを25回繰り返せば、私たちが知りたい厚さが計算できますね。

一体、どのくらいになるのでしょうか？

下の表が、A4コピー用紙を25回折った時の厚さの計算結果です。左側から、折った回数、厚さ(mm)と、右端は厚さをメートル換算した結果を載せています。

これをスルスルとスクロールして、25回折った時の厚さを見てみると…。

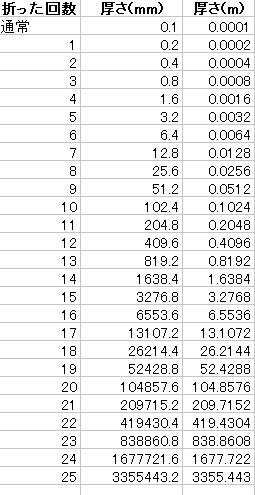
25回のところは、3355443.2(mm)と書かれています。
センチメートルに直すと33554.43(cm)です。メートルに直すと3355.443(m)。

富士山の高さが3776mですから、A4のコピー用紙1枚を半分ずつ25回折ると、ほぼ富士山の高さに匹敵するほどの厚さになることがわかります。

厚さ0.1mmのコピー用紙でも、富士山の高さにするマジック

20世紀の天才と呼ばれるアルベルト・アインシュタインは、次のような言葉を残しています。

「数学における最も偉大な発見は、複利の力である」
(アルベルト・アインシュタイン)

たった厚さ0.1mmのコピー用紙を富士山の高さにするための秘密が、この複利のメカニズムに隠されています。

アルベルト・アインシュタインも認めた複利という仕組みとは、一体どのような力を持っているのでしょうか？

複利を動かす基本的なメカニズム

複利の公式は次のとおりです。

新しい値　＝　元の値 ＋ 元の値 × 利率

わかりやすく直すと、

新しい値　＝　元の値 × (1＋利率)

これで、1回分の値が計算できます。

たった1回だけだと元の値と利率のみで評価しがちですが、より重要なのは、複利は繰り返しができるという点です。
繰り返すことで1回1回の変化量は少なくても、確実な成長を産み出すことができるわけです。

複利という仕組みを動かすのは、元の値や利率だけでなく『何回繰り返せるか？』であり、繰り返した回数や時間を使った継続性にあります。

つまり、私たちが複利の力をうまく活かすためには、

1. 元の値(初期値)
2. 利率
3. 繰り返した回数

の3つが必要になります。これらはすべて掛け算なので、どれかがゼロなら結果もゼロです。
逆に、3つのうち2つの数値が0ではないが、凄く小さな数字だったとしても、残りの1つが巨大な数値であれば、結果も大きなものになります。

始めは小さくてもいい。大事なのは、成長性と継続性。

厚さ0.1mmのコピー用紙が富士山の高さに匹敵するのは、非常に小さい元の値(紙の厚さ0.1mm)で始めたとしても、利率が2倍と高い(常に半分に折る)からであることと、25回繰り返したことです。

グラフにすると、このようになります。

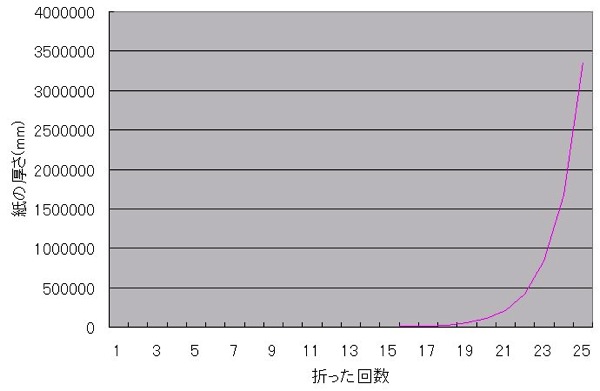
見てわかる通り、このスケールでは16回目まではグラフも描画されていないほど小さな変化です。しかし、19回目まではほとんどの変化がないグラフが20回目以降になって、急激な伸びを示し始めます。

実は、目標達成もこれと同じ仕組みです。

あなたが今年、自分が決めた目標を達成するために何かの行動を25回繰り返すとしたら、目に見えた変化が出てくるのは16回目以降です。

しかも、現実は、コピー用紙とは違って何回繰り返せばゴールに辿り着くのかもわからない状況です。

多くの人はその時点で諦めてしまいます。なぜなら、今結果が出ているのか出ていないのかわからないし、何回繰り返せばゴールに辿り着けるのかもわからないから。ダイヤモンドを求め、炭鉱を掘り進む人にとって、目の前に見えるのは、ゴツゴツとした岩ばかり。あとどのくらいでダイヤにたどり着くかは、横から見ない限り見えないのです。

でも、そんな時にこそ「A4サイズの1枚の紙を25回折ったら、厚さは何センチになるか？」と思い出してみて欲しいのです。複利の仕組みが私たちに教えてくれることは、

『誰しもどんな状況から始めようが、小さな成長と繰り返しによって、大きな力を手に入れることができる』という普遍的な事実です。

ゴールまでの地図がわからず、目の前が見えないときにこそ、この複利のメカニズムを思い出して欲しいのです。

成功と目標達成のキーワードである成長と繰り返しを使って、あなたの目標が実現されることを願っています。